Trigonometri Nedir? Temel Kavramlar ve Uygulamaları

Trigonometri, matematiğin en temel ve en heyecan verici dallarından biri olup, üçgenlerin kenarları ve açıları arasındaki karmaşık ancak düzenli ilişkileri inceler. Gökbilimden mühendisliğe, müzik teorisinden bilgisayar grafiklerine kadar modern dünyayı şekillendiren pek çok teknolojinin arkasında trigonometrik hesaplamalar yatar. Bu bilim dalı, sadece akademik bir uğraş değil, fiziksel dünyayı anlamlandırmamızı sağlayan evrensel bir dildir.
- Trigonometrinin temel tanımını ve tarihsel gelişimini kavrayacaksınız.
- Açı ölçü birimleri olan derece ve radyan arasındaki farkları ve dönüşümleri öğreneceksiniz.
- Dik üçgen üzerindeki temel trigonometrik oranları (sinüs, kosinüs, tanjant, kotanjant) tanımlayabileceksiniz.
- Birim çember mantığını ve trigonometrik fonksiyonların bölgelere göre işaretlerini analiz edeceksiniz.
- Trigonometrinin günlük hayattaki ve bilimsel alanlardaki uygulama örneklerini keşfedeceksiniz.
- Köken: Trigonometri kelimesi Yunanca ‘trigonon’ (üçgen) ve ‘metron’ (ölçmek) kelimelerinden türetilmiştir.
- Temel Araç: En büyük yardımcınız hipotenüsü 1 birim olan dik üçgenler ve birim çemberdir.
- Fonksiyonlar: Sinüs ve kosinüs temel fonksiyonlar; tanjant, kotanjant, sekant ve kosekant ise türetilmiş fonksiyonlardır.
- Kritik Sabit: Radyan hesaplamalarında ‘Pi’ (π) sayısı vazgeçilmezdir.
Trigonometrinin Tanımı ve Tarihsel Yolculuğu
Trigonometri, matematiğin üçgenlerin kenar uzunlukları ve açıları arasındaki bağıntıları konu edinen bir alt dalıdır. İnsanlık tarihi boyunca denizcilerin rotalarını belirlemesi, mimarların devasa yapılar inşa etmesi ve astronomların yıldızlar arasındaki mesafeleri ölçmesi hep bu disiplin sayesinde mümkün olmuştur. Antik Mısır ve Mezopotamya’da piramitlerin yapımı sırasında temel düzeyde kullanılan bu bilgiler, Antik Yunan’da Hipparchus tarafından sistemleştirilmiştir.
Orta Çağ’da ise İslam dünyasındaki matematikçiler trigonometriye altın çağını yaşatmıştır. Battani, El-Biruni ve Nasreddin Tusi gibi isimler, küresel trigonometriyi geliştirerek ve fonksiyonları daha hassas hesaplayarak modern matematiğin temellerini atmışlardır. Bugün kullandığımız sinüs ve kosinüs kavramları, bu uzun ve zengin tarihsel sürecin bir meyvesidir.
Açı Ölçü Birimleri: Derece ve Radyan
Trigonometrik hesaplamalara başlamadan önce, açıları nasıl ölçtüğümüzü anlamak hayati önem taşır. Günlük hayatta en sık kullandığımız birim derece olsa da, bilimsel ve teknik hesaplamalarda radyan çok daha işlevseldir. Bir tam çemberin 360 eşit parçaya bölünmesiyle elde edilen her bir parçaya 1 derece denir. Radyan ise, çemberin yarıçapı uzunluğundaki bir yayın merkez açısını ifade eder.
Derece ve radyan arasındaki dönüşüm, matematiğin en temel formüllerinden biridir. 180 derecenin π radyana eşit olduğu gerçeğinden yola çıkarak her türlü dönüşümü yapabiliriz. Örneğin, 90 derece π/2 radyana, 60 derece ise π/3 radyana karşılık gelir. Sınavlarda ve problem çözümlerinde bu iki birim arasındaki geçişleri hızlıca yapabilmek size büyük zaman kazandıracaktır.
Dik Üçgende Trigonometrik Oranlar
Trigonometrinin kalbi dik üçgenlerde atar. Bir dik üçgende, 90 derecelik açının karşısındaki en uzun kenara hipotenüs adı verilir. Diğer iki kenar ise dik kenarlardır. Bir açının trigonometrik değerlerini bulmak için bu kenarların birbirine olan oranlarını kullanırız. Bu oranlar, açının büyüklüğüne göre değişen ancak üçgenin boyutundan bağımsız olan sabit değerlerdir.
- Sinüs (sin): Karşı dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır.
- Kosinüs (cos): Komşu dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır.
- Tanjant (tan): Karşı dik kenarın komşu dik kenara oranıdır (aynı zamanda sin/cos).
- Kotanjant (cot): Komşu dik kenarın karşı dik kenara oranıdır (aynı zamanda cos/sin).
| Fonksiyon | Formül (Dik Üçgen) | Kısaltma |
|---|---|---|
| Sinüs | Karşı / Hipotenüs | sin(x) |
| Kosinüs | Komşu / Hipotenüs | cos(x) |
| Tanjant | Karşı / Komşu | tan(x) |
Birim Çember ve Fonksiyonların İşaretleri
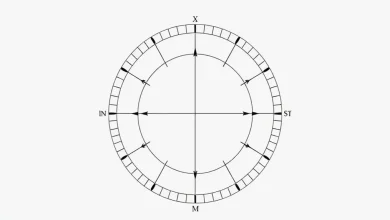
Trigonometriyi sadece dik üçgenlerle sınırlamak, geniş açılar (90 dereceden büyük olanlar) için yetersiz kalır. İşte bu noktada birim çember devreye girer. Merkezi başlangıç noktası (0,0) olan ve yarıçapı 1 birim olan çembere birim çember denir. Bu çember üzerinde alınan bir noktanın x koordinatı kosinüs değerini, y koordinatı ise sinüs değerini verir.
Birim çember dört bölgeye ayrılır. Birinci bölgede (0-90°) tüm fonksiyonlar pozitif değerler alırken, ikinci bölgede (90-180°) sadece sinüs pozitiftir. Üçüncü bölgede (180-270°) tanjant ve kotanjant pozitif, dördüncü bölgede (270-360°) ise sadece kosinüs pozitiftir. Bu işaretleri bilmek, karmaşık trigonometrik denklemleri çözerken hata yapmanızı engeller.
30 derecelik bir açının sinüs değerini bulalım. Standart bir 30-60-90 üçgeninde, 30 derecenin karşısındaki kenar hipotenüsün yarısıdır. Dolayısıyla sin(30°) = 1/2’dir. Aynı açının kosinüs değeri ise √3/2 olarak hesaplanır.
Temel Trigonometrik Özdeşlikler
Matematikte bazı eşitlikler vardır ki bunlar her zaman doğrudur. Trigonometride en meşhur özdeşlik, Pisagor Teoremi’nin bir türevi olan sin²x + cos²x = 1 eşitliğidir. Bu formül, bir açının sinüsünü biliyorsanız kosinüsünü (veya tam tersini) bulmanızı sağlar. Ayrıca tanjant ile kotanjantın çarpımının 1 olduğu (tanx * cotx = 1) bilgisi de sadeleştirme sorularında sıkça kullanılır.
Bu özdeşlikler, karmaşık görünen trigonometrik ifadeleri daha basit hale getirmek için kullanılan birer ‘anahtar’ gibidir. Özellikle türev ve integral gibi ileri matematik konularında bu dönüşümler hayat kurtarıcı rol oynar. Özdeşlikleri ezberlemek yerine, birim çember üzerindeki mantığını anlamak kalıcı öğrenme sağlar.
Trigonometrinin Günlük Hayat ve Bilimdeki Uygulamaları
Trigonometri sadece kağıt üzerinde kalan bir ders konusu değildir. Bugün kullandığımız pek çok teknoloji bu hesaplamalara dayanır. Örneğin, GPS sistemleri konumunuzu belirlemek için uydularla aranızdaki açıyı ve mesafeyi trigonometrik yöntemlerle hesaplar. Mimarlar, bir binanın güneş ışığını en verimli şekilde alması için çatı eğimini bu fonksiyonlarla belirler.
Ayrıca, ses ve ışık dalgaları birer sinüs dalgası şeklinde hareket eder. Müzik prodüksiyonunda seslerin temizlenmesi, tıpta EKG cihazlarının kalp atışlarını analiz etmesi veya okyanuslardaki gelgit olaylarının tahmin edilmesi tamamen trigonometri sayesindedir. Oyun geliştiriciler ise karakterlerin akıcı bir şekilde hareket etmesi ve gerçekçi fizik kurallarının uygulanması için sürekli olarak bu formülleri kullanır.
- Bir dik üçgende karşı kenar 3 birim, komşu kenar 4 birim ise bu açının sinüs değeri kaçtır?
- 90 derecelik bir açı radyan cinsinden nasıl ifade edilir?
- Hangi bölgede hem sinüs hem de kosinüs fonksiyonları negatif değer alır?
- tan(x) * cot(x) işleminin sonucu her zaman kaçtır?
- Trigonometri, üçgenlerin açı ve kenar ilişkilerini inceleyen temel bir matematik dalıdır.
- Temel fonksiyonlar olan sinüs, kosinüs, tanjant ve kotanjant dik üçgen oranları ile tanımlanır.
- Birim çember, açıların 360 dereceye kadar ve ötesindeki değerlerini anlamamıza yardımcı olur.
- Derece ve radyan dönüşümleri (180° = π) hesaplamaların temelini oluşturur.
- Bilim, mühendislik ve günlük yaşamda geniş bir uygulama alanına sahiptir.
Öğrendiklerinizi Pekiştirin
Trigonometri konusunu tam anlamıyla kavradığınızda, sadece matematik dersinde başarılı olmakla kalmayacak, aynı zamanda çevrenizdeki dünyayı daha farklı bir gözle görmeye başlayacaksınız. Bu temel kavramları öğrendikten sonra, bir sonraki adımınız toplam-fark formülleri, yarım açı formülleri ve trigonometrik denklemler olmalıdır. Unutmayın, her büyük başarı küçük ve sağlam adımlarla başlar. Bol bol pratik yaparak ve birim çember üzerinde görselleştirmeler yaparak bu konuyu ustalıkla çözebilirsiniz.